Arknights Pull Analysis
This post aims to employ mathematical modeling to estimate the expected number of pulls required to obtain a single random 6-star character in the mobile game Arknights. Feel free to utilize the provided catalog on the right-hand side to navigate to the specific sections that pique your interest.
What is Arknights
Arknights[1] is a popular mobile tower defense game where players take on the role of a “Doctor” leading a team of unique operators to defend against threats in a dystopian world.
The game incorporates a gacha system that revolves around acquiring new operators through randomized draws, each with designated probabilities. Operators are categorized by their star ratings, with 6-star operators considered the most powerful and 1-star operators the least. The probability of obtaining a 6-star operator stands at 2% per roll by default, although exceptions may apply as detailed below:
In-game description of the pity system:
If you do not roll a 6-star operator after 50 rolls, the probability of obtaining a 6-star Operator on the next roll will be increased from 2% to 4%. If you still do not roll a 6-star Operator, the probability of obtaining a 6-star Operator on the next row will be further increased from 4% to 6%, and this process repeats until a maximum probability of 100%, at which point you are guaranteed to receive a 6-star Operator.
The Problem
We know the probability of obtaining a six-star unit in Arknights upon each individual roll, but we do not know the expected number of rolls required to obtain a six-star unit.
Knowing the expected value of obtaining a six-star is important because players need to determine the amount of Orundum (Arknights’ Gacha currency) they need to accumulate prior to event banners in order to safely secure their desired operators. This question is increasingly relevant, particularly with the recent launch of the Limited Event “IL Siracusano”.
Numerous attempts have been made to tackle this problem, such as utilizing the Monte Carlo Approach or running Exploratory Data Analysis. In this post, I will attempt to construct a mathematical model via binomial distribution, offering another perspective on this intriguing problem.

Modeling the 1st to 50th Roll
To establish our model, it’s important to consider that we are guaranteed to obtain a six-star unit by the 99th roll as our success rate will have increased to 100% by that point. Therefore, our focus lies within the range of the 1st to 99th rolls, as our objective is to secure a single 6-star Operator.
To apply the binomial distribution, we must ensure that four conditions are met:
- A fixed number of rolls
- Independence between each roll
- Two possible outcomes (success or failure) for each roll
- A constant probability of success throughout
The binomial distribution equation is expressed as:
$$
P_{x}=\left(\begin{array}{l}n \ x\end{array}\right) p^{x} q^{n-x}
$$
where $P$ represents the binomial probability. In our case, we are interested in determining the average number of rolls required to obtain a single six-star unit, so $x$ is set to 1. The probability of success on a single roll $p$ is 2%, while the probability of failure $q$ is 98%. The number of trials $n$ is confined to the range of 1 to 50, as we are focusing on the 1st to 50th rolls exclusively. By defining all these variables, we have completed the formulation of our binomial distribution equation:
$$
P_{1 \text { six star }}=\mathrm{n} \times 0.02 \times 0.98^{n-1}, \quad 1 \leq n \leq 50
$$
However, $P$ in the binomial distribution equation represents the probability of obtaining a six-star unit within any of the $n$ trials. This is not aligned with our objective, as we are specifically interested in the probability of obtaining a six-star unit at the $n$ th roll alone, assuming all previous rolls have failed. The order of selection is crucial here because our calculation concludes as soon as we secure a single six-star unit. Consequently, we need to adjust our equation by dividing it by $n$ to account for only one combination being considered:
$$
P_{1 \text { six star on the nth roll only }}=\mathrm{n} \div \mathrm{n} \times 0.02 \times 0.98^{n-1}, \quad 1 \leq n \leq 50
$$
By simplifying and expressing the equation as a function, we obtain:
$$
P(n)=0.02 \times 0.98^{n-1}, \quad 1 \leq n \leq 50
$$
Modeling the 51st to 99th Roll
For the 51st to 99th roll, our success rate progressively increases by 2% per roll. This means that the 51st roll has a 4% success rate, the 52nd roll has a 6% success rate, and so on, until reaching the 99th roll with a success rate of 100%.
Since the success rate is no longer fixed, we need to transition away from using the binomial distribution as our model. Given my limited knowledge and unfamiliarity with any theorems regarding scenarios with changing probabilities, it is evident that we need to devise our own function to effectively model this situation.
Considering the fixed increase in success rate, it is highly probable that there exists a discernible relationship when evaluating the probability of each individual roll. As the success rate remains fixed on an individual roll basis, we can effectively employ the binomial distribution to calculate the probability of obtaining a six-star unit with each roll.
Let’s start with the 51st roll. Referring to our function for the 1st to 50th roll, our $x$ value along with our number of combinations remains constant. Our probability of success $p$ will be set to 4% as mentioned before. However, our probability of failure $q$ will not be set to 96%. If we set $q$ to 96%, we are stating that the probability of failure for all rolls before 51st is 96%, which is not true. Referring to our binomial function for the 1st to 50th roll $P(n)=$ $0.02 \times 0.98^{n-1}$, we notice that we only apply our failure probability for $n-1$ rolls. Applying the same concept for the 51st term, we are only concerned with the probability of failure for the 1st to 50th term. Since the probability of failure is constant for the 1st to 50th term, our probability of failure component of the 51st roll is $0.98^{50}$. After defining all our variables, our equation of the 51st roll is complete:
$P(51)=0.04 \times 0.98^{50}$
Moving on to the 52nd term, the probability of success increases to 6%. As for the probability of failure, we apply the same principle of calculating it only for the $n-1$ rolls. Consequently, we arrive at a value of $0.96 \times 0.98^{50}$. The 0.96 represents the probability of failure for the 51st roll, while $0.98^{50}$ refers to the probability of failure for the 1st to 50th rolls. With all variables defined, the equation for the 52nd roll is now complete:
$P(52)=0.06 \times 0.96 \times 0.98^{50}$
Following the same procedure:
$P(53)=0.08 \times 0.94 \times 0.96 \times 0.98^{50}$
$P(54)=0.10 \times 0.92 \times 0.94 \times 0.96 \times 0.98^{50}$
$P(55)=0.12 \times 0.90 \times 0.92 \times 0.94 \times 0.96 \times 0.98^{50}$
···
$P(98)=0.98 \times 0.04 \times 0.06 \times \ldots \times 0.94 \times 0.96 \times 0.98^{50}$
$P(99)=1 \times 0.02 \times 0.04 \times 0.06 \times \ldots \times 0.94 \times 0.96 \times 0.98^{50}$
From the derived equations, we can extract the probability of success component as follows:
$(0.02+0.02(n-50)), \quad 51 \leq n \leq 99$
Simplifying to:
$0.02(n-49), \quad 51 \leq n \leq 99$
The probability of failure component can be expressed as a product of an arithmetic series, where the probability of failure decreases by 0.02 for each subsequent roll. Following the formula for the product of an arithmetic series:
$\prod_{k=0}^{n-1}\left(c_{1}-k d\right)$
Here, $n$ represents the number of rolls, $c_{1}$ is the first term, and $d$ is the common difference. In our case, $k$ will be 51 since our function starts from the 51st roll, $c_{1}$ will be 0.98, and $d$ will be -0.02. Therefore, the probability of failure component in our function is derived as:
$$
\prod_{k=51}^{n-1}(0.98-0.02(k-50)), \quad 50<n \leq 99
$$
The notation $k − 50$ indicates that we are treating the 51st roll as the first roll in our equation for the 51st to 99th rolls. This notation can be simplified as follows:
$$
\prod_{k=51}^{n-1}(1.98-0.02 k), \quad 50<n \leq 99
$$
Combining each component, we can arrive at the final form of our function for the 51st to 99th rolls:
$$
P(n)=0.02(n-49) \times 0.98^{50} \times \prod_{k=51}^{n-1}(1.98-0.02 k), \quad 50<n \leq 99
$$
It is important to note that the power notation is structured in a way that for the 51st roll, the initial roll is 51, and the number of rolls is 50. This arrangement results in a value of 1, which is intentionally set up as our probability of failure component for the 51st roll is only $0.98^{50}$.
With this clarification, our mathematical model is now complete:
$$
P(n) =
\begin{cases}
0.02 \times 0.98^{n-1}, & 1 \leq n \leq 50 \\
0.02 \times (n-49) \times 0.98^{50} \times \prod_{k=51}^{n-1}(1.98-0.02k), & 50 < n \leq 99
\end{cases}
$$
Graphing the Model
We can create a graph to provide a visual representation of the Arknights character pulling model:
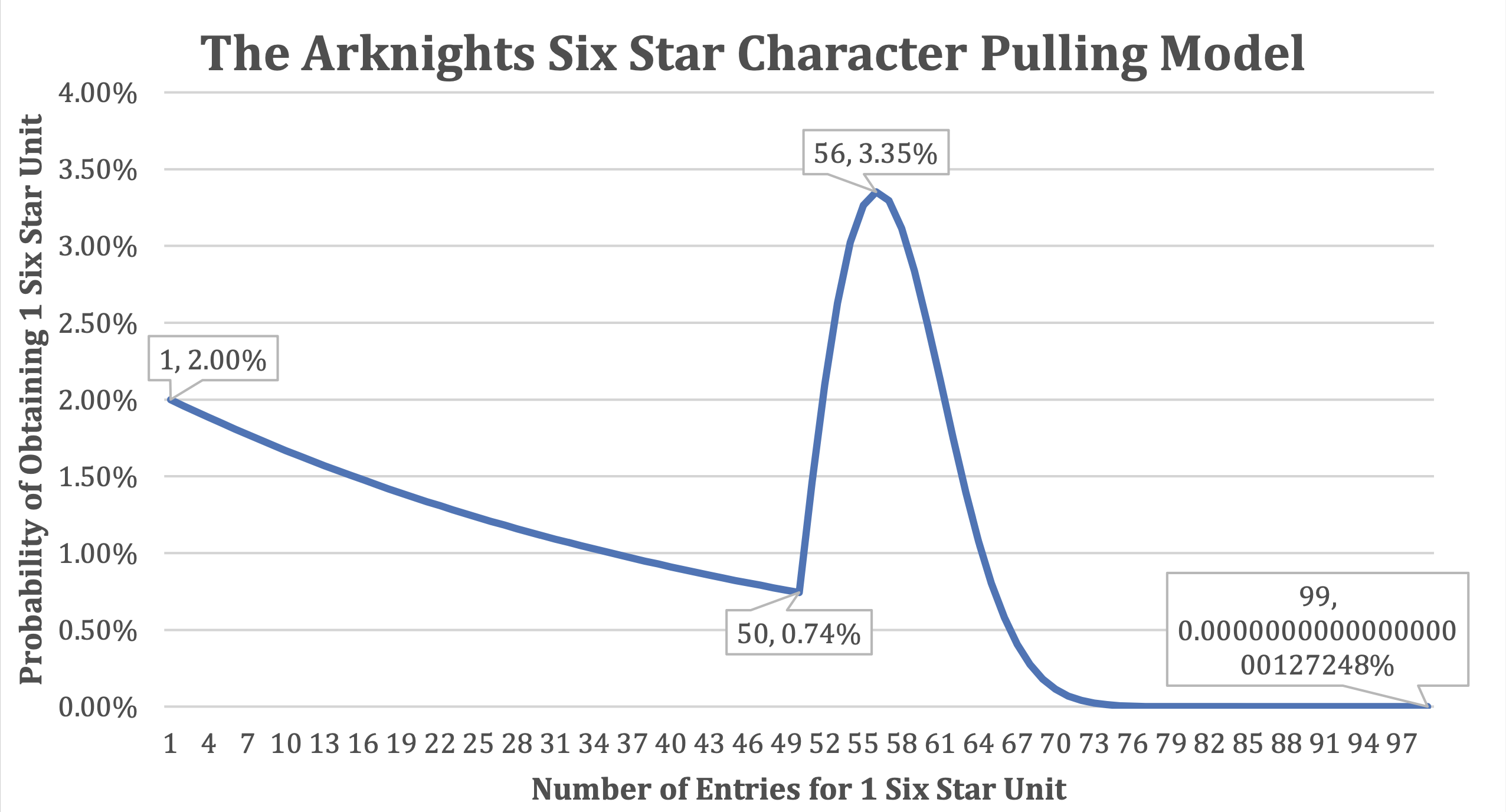
This graph demonstrates the probability of obtaining a six-star unit on the $n^{th}$ roll. Examining the graph, we observe that the initial probability of obtaining a six-star is 2%, which serves as our base probability. As subsequent rolls are considered, the probability gradually decreases. This decline is expected, as it indicates that all previous rolls leading up to the successful pull were unsuccessful. The downward trend persists until the 50th roll, where the probability reaches 0.74%.
At the 51st roll, the pity system activates, resulting in an upward slope. This upward slope indicates that the pity system is functioning as intended, offering higher probabilities for obtaining a six-star unit. The peak probability of 3.35% occurs at the 56th roll. Following this peak, the probability gradually declines, reflecting the impact of the pity system and previous successful rolls.
Notably, reaching the 99th roll without obtaining a six-star unit is highly unlikely, with a probability close to 0. Conclusively, most players will achieve success before reaching the later stages of the character pulling system. However, it’s worth noting that the 56th roll, despite having the highest probability, does not represent the average roll number we are seeking.
Solution 1: Cumulative Probability
One approach to determining the average number of rolls required to obtain one six-star unit is to calculate the cumulative probability based on the aforementioned model. The cumulative probability at 50% can serve as an indicator of the average roll, as it signifies that half of the player base has already achieved success in obtaining one six-star unit.
Using sigma notation to compute the cumulative probability, we obtain:
$\text { Cumulative Probability }=\sum_{i=1}^{n} P(i), \quad 1 \leq n \leq 99$
Graphically representing this equation provides further clarity: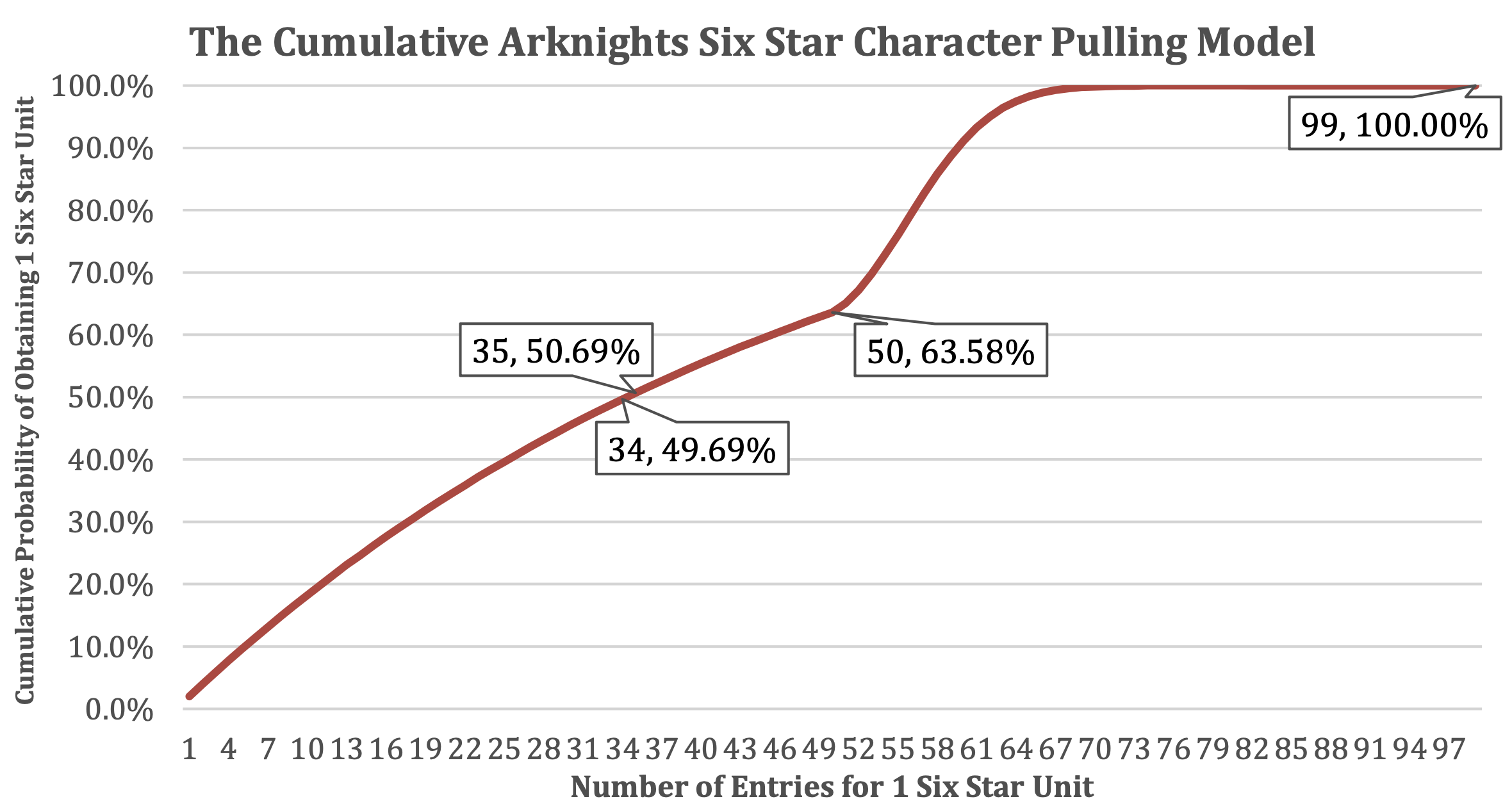
Upon analyzing the graph, it becomes evident that the cumulative probability reaches 100% at the 99th roll, affirming the accuracy of our equation and model. This validates that the individual probabilities for each roll were calculated correctly, resulting in a cumulative sum of 100%.
Additionally, the slope of the graph increases notably after the 50th roll, indicating a higher rate of players successfully obtaining a six-star unit due to the implementation of the pity system.
At the 35th roll, the cumulative probability stands at 50.69%. This figure represents the average number of rolls required with 50% denoting the point at which half of the player base is expected to have achieved success in obtaining a six-star unit.
Solution 2: Expected Values
Another approach to determine the average roll is by calculating the expected values, which represent the mean of a probability distribution. For our case of pulling one six-star unit, we can apply the expected value formula. Considering a random variable $X$ with possible rolls $e_{1}, e_{2}, e_{3}, \ldots, e_{n}$ and associated probabilities $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$, the expected value of $X$ is given by:
$E(X)=\sum_{i=1}^{n}\left(e_{i} \times a_{i}\right)$
To calculate the expected value of pulling one six-star unit, we set $e_{i}$ as $i$, since the number of rolls corresponds to the number of trials. The $a_{i}$ values are set as $P(n)$, representing the probability of obtaining one six-star unit for each individual trial. The total number of trials $n$ is set to 99. Therefore, the equation becomes:
$E(\text { Pulling } 1 \text { Six Star })=\sum_{i=1}^{99}(i \times P(i))$
Solving this equation yields the result:
$E(\text { Pulling } 1 \text { Six Star })=34.59$
Hence, the average number of rolls required to obtain one six-star unit is approximately 34.59 pulls. This outcome aligns with our cumulative graph, falling between the 34th roll at 49.69% and the 35th roll at 50.69%.
Conclusion
Both solutions lead to a similar conclusion (34.59%), which aligns with the cumulative probability graph reaching 100%, as well as other methods like the previously mentioned Monte Carlo approach and code simulations.
Taking 35 as the average roll, since rolls are whole numbers, and considering each roll has a cost of 600 Orundum, the average cost of obtaining a six-star unit is 600 × 35 = 21,000 Orundum.
Additionally, I have created an Arknights Pull Quantile table: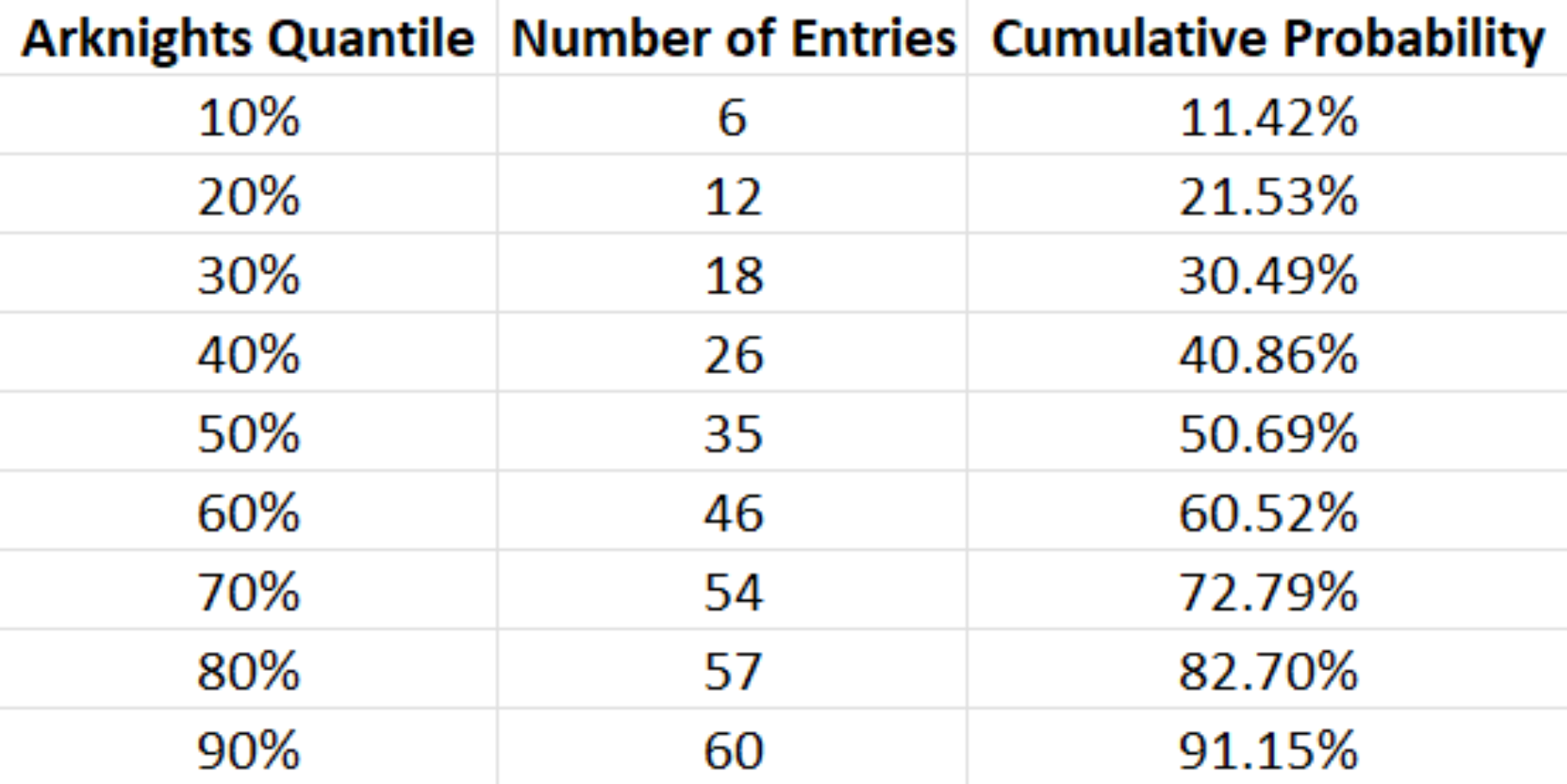
Using this table, I can determine my “luckiness” based on the number of rolls. For example, in the IL Siracusano Event Banner, where I obtained a six-star unit (Texalter) in 26 rolls, I am ranked in the top 40.86% within the player base. This means that I am luckier than approximately 60% of the gamer population :)
Evaluations and Extensions
The process of finding relationships between individual rolls and solving the complex probability problem unfolded as expected. The presented models accurately illustrate the binomial outcome and cumulative probability in obtaining a six-star unit.
However, I made several mistakes regarding the probability of failure component during the process. It was only when I graphed the cumulative probability that I realized something was amiss. Through multiple iterations and edits, I eventually reached a cumulative probability of 100%. Each adjustment allowed me to gain a deeper understanding of the binomial distribution and the contributions of each component in arriving at the solution.
This investigation can be extended in various directions. Firstly, exploring additional methods to calculate average roll amounts would be valuable. For example, incorporating the Markov property, which accounts for the dependence of a certain roll’s probability on the outcomes of previous rolls, could offer an intriguing alternative for determining the average roll.
Another potential extension involves calculating the binomial probability of obtaining a specific six-star unit instead of any six star. This requires accounting for the unique rate of each six-star unit. Consequently, the mathematical model would be adjusted to factor in the varying probabilities associated with each operator.
Additionally, examining the economic aspect of Arknights and the distribution of the in-game currency Orundum among players could provide valuable insights into player behavior and spending patterns.
Overall, this post contributes to the growing knowledge base about Arknights, offering a mathematical approach to address the complex issue of obtaining six-star units. Utilizing mathematical modeling techniques, the solutions presented provide players with a better understanding of the game’s mechanics and the resources required to secure their desired operators.
If you have any questions or would like to explore this topic further, please do not hesitate to reach out. I would be delighted to delve into further analyses or explore new directions related to Arknights and probability modeling.
Bibliography
- Arknights (n.d.). Retrieved 20 May 2023, from https://www.arknights.global ↩